Feigenbaumdiagramm
Das Feigenbaumdiagramm leitet sich aus der logistischen Gleichung ab und bildet eine Periodenverdopplungsbifurkation ab. Bei kleinen Parameterwerten existiert nur ein stabiler Fixpunkt, der am ersten Bifurkationspunkt in einen Orbit aus zwei alternierenden Fixpunkten übergeht. Dieser Orbit verdoppelt dann an weiteren Bifurkationspunkten jedes Mal wieder seine Periode (kommt also erst nach 2, 4, 8, etc. Durchläufen wieder an den gleichen Punkt), bis er bei einem Parameterwert von etwa 3,57 in einen chaotischen Zustand übergeht, wo überhaupt keine Periode mehr erkennbar ist. Die Abbildung ist durch diese Darstellung gut als solche zu untersuchen, nicht jedoch um die Dynamik bei einem bestimmten r darzustellen. Man erhält ein Feigenbaumdiagramm in dem man die Werte für große n (z.B. x600 bis x900) in Abhängigkeit der r-Werte einträgt. Es stellt dann den Endzustand der Orbits dar, die sich an die Attraktoren angenähert haben.
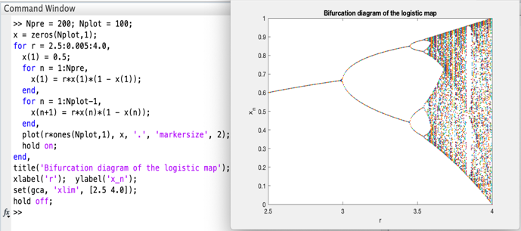
Abb. 5: Feigenbaum – Diagramm
Deterministisches Chaos
Deterministisches Chaos ist das zufällig erscheinende Verhalten von dynamischen Systemen, welches vorherbestimmten Regeln folgt. Dabei wird das chaotische Verhalten jedoch nicht durch äußere Umstände oder Störungen verursacht, sondern folgt aus dem Verhalten des Systems. Der chaotische Zustand ist nicht reproduzierbar, trotz deterministischer Dynamik. Das heißt für chaotische Systeme führen langfristig ähnliche Startbedingungen nicht zu ähnlichen Wirkungen, obwohl die Folgewerte der Funktion eindeutig berechenbar sind. Das Problem ist, das in Experimenten eigentlich von einem schwachen Kausalitätsprinzip ausgegangen, indem gleiche Ursachen auch die gleiche Wirkung haben. Da aber in einem Experiment unter realen Bedingungen nie alle Ausgangsbedingungen gleich sind, geht man von einem starken Kausalitätsprinzip aus, welches besagt: Ähnliche Ursachen haben ähnlich Wirkung. Das dadurch auch nicht jedes Experiment belegt werden kann, zeigt dieses Beispiel. Daher geht man von verletzter starker Kausalität aus. Bei logistischen Gleichungen spricht man von der sensitiven Abhängigkeit der Anfangsbedingungen und lässt sich auf die Streck- und Falteigenschaften der Gleichung zurückführen. Die Entwicklung eines chaotischen dynamischen Systems ist als Folge der Unvermeidbarkeit von Messfehlern bei der Bestimmung des Anfangszustandes nicht vorhersehbar, nicht aufgrund eines stochastischen Verhaltens.
Strogatz, S. (1994). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering. Perseus Books Group
Poser, H. (2012). Wissenschaftstheorie. Eine philosophische Einführung. Stuttgart 2012,5, S. 293–295.
Krabs, W. (1998). Dynamische Systeme: Steuerbarkeit und chaotisches Verhalten. B.G.Teubner, Leipzig