Music and mathematics are closely linked and an example of their common path are the so-called Euclidean rhythms.
As the name suggests, its roots go back to the Greek mathematician Euclid (around 300 BC). In his text “Elements” a revolutionary algorithm is described to efficiently find the greatest common divisor (GCF) of 2 integers.
Here an example on how it works [2]
[
The Euclidean Algorithm for finding GCD(A,B) is as follows:
If A = 0 then GCD(A,B)=B, since the GCD(0,B)=B, and we can stop.
If B = 0 then GCD(A,B)=A, since the GCD(A,0)=A, and we can stop.
Write A in quotient remainder form (A = B⋅Q + R)
Find GCD(B,R) using the Euclidean Algorithm since GCD(A,B) = GCD(B,R)
Example:
Find the GCD of 270 and 192
A=270, B=192
A ≠0
B ≠0
Use long division to find that 270/192 = 1 with a remainder of 78. We can write this as: 270 = 192 * 1 +78
Find GCD(192,78), since GCD(270,192)=GCD(192,78)
A=192, B=78
A ≠0
B ≠0
Use long division to find that 192/78 = 2 with a remainder of 36. We can write this as:
192 = 78 * 2 + 36
Find GCD(78,36), since GCD(192,78)=GCD(78,36)
A=78, B=36
A ≠0
B ≠0
Use long division to find that 78/36 = 2 with a remainder of 6. We can write this as:
78 = 36 * 2 + 6
Find GCD(36,6), since GCD(78,36)=GCD(36,6)
A=36, B=6
A ≠0
B ≠0
Use long division to find that 36/6 = 6 with a remainder of 0. We can write this as:
36 = 6 * 6 + 0
Find GCD(6,0), since GCD(36,6)=GCD(6,0)
A=6, B=0
A ≠0
B =0, GCD(6,0)=6
So we have shown:
GCD(270,192) = GCD(192,78) = GCD(78,36) = GCD(36,6) = GCD(6,0) = 6
GCD(270,192) = 6
] [2]
Its application in music and their formal discovery is attributed to the computer scientist Godried Toussint in 2004.
He found that this algorithm could be translated into rhythms.
But how? The GCF could be used to distribute a determined number of onsets across a determined number of step.
These rhythms are often represented with a circular visualization.
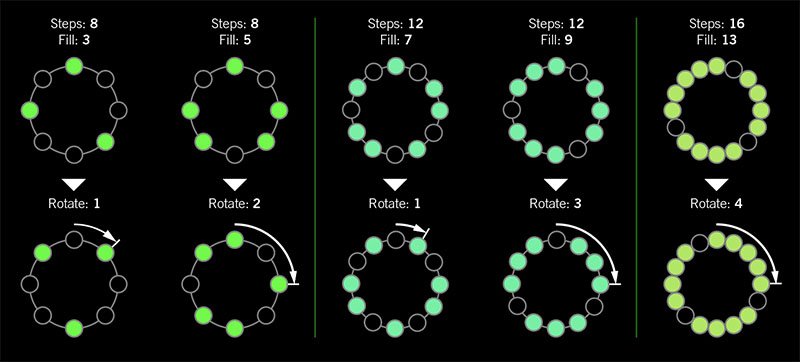
So, as we can see, the Euclidean rhythm needs a number of onset (filling) uniformly distributed over a number of steps (per measure).
Here’s an example of what it might sound like:
When combining more of them, we have a polyrhythm, a groove that consists of two or more contrasting rhythms playing simultaneously.
What is truly amazing is that music and mathematics are not only connected theoretically, but also viscerally.
Indeed, many rhythms found in cultures and in history are actually naturally Euclidean.
Brazillian Bossa nova = 5 onsets distributed across 16 steps
Cuba’s Tresillo = 3 onsets distributed across 8 steps.
Turkey’s Aksak rhythm = 4 onsets distributed across 9 steps.
and many more.
And, of course, an example in Radiohead’s music:
References
[1] Harrison Shimazu – What are Eucledian rhytms?
[2] Kan Academy – The Euclidean Algorithm