What is really the sound of fire? In general, the fire should not make any sound, what we hear is more the burning object or the air itself, the so-called crackling and hissing.
Sound is defined as oscillation in pressure, particle displacement and velocity propagated in medium such as air or water, that have density.
On the other hand, thermal conduction, hence the transfer of heat (energy) resulting from temperature differences, occurs through the random movement of atoms or molecules.
Heat is vibration of molecules, but it takes a very large amount of molecules moving organized together to create what we perceive as sound, as we perceive the vibration of the air as a whole, not of individual molecules.
Thus, the combustion itself does not produce any sound, but due to the release of a high amount of energy, nearby molecules acquire a greater random kinetic energy which allows us to perceive a so-called Brownian noise.
Brownian noise (or Brown Noise), is a noise characterized by the decrease of 6 dB per octave with increasing density.

Normally, we detect longitudinal waves, as they are made up of groups of particles that periodically oscillate with high amplitudes, so we can easily detect, for example, a human voice.
In the event of combustion due to the disorganized movement of the particles, the power at the eardrum is lower and this noise is not audible. This means that we mainly hear the popping of wood or the sound of the wind blowing as the air expands and rises.
Increasing the temperature leads to an increase in the average kinetic energy of the molecules, and thus increases the pressure.
Therefore, we could try to find the hypothetical temperature necessary for the Brownian noise produced by a fire to be audible.
In the work from Sivian and White [2] the minimum audible field (MAF) was determined, that is the thresholds for a tone presented in a sound field to a participant who is not wearing headphones.
Here we can also find a formula to express it:
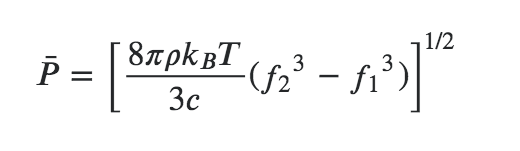
P is the RMS value, and we could consider it as P = 2 x 10^-2 (so 60 dB, as loud as a conversation);
𝜌 (Rho) is the density of air (1.225 kg/m^3);
kB is the Boltzmann constant (1.38064852 × 10^-23 m^2 kg s^-2 K^-1);
T is the temperature, in Kelvin
c is the speed of sound in air (344 m/s),
f1 and f2 are the frequency range. Let’s consider the audible range of 20-20000 Hz.
So we need to do the inverse formula to find T:
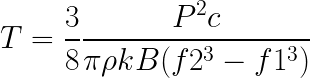
After all the calculations and after converting all the data to common values, the result is T= 88.144,20 K. An incredibly high temperature, much higher than the sun’s core! (5.778K)
Of course we can hear Brownian noise by simply generating it in any DAW and getting it to 60dB, yet we wouldn’t hear the noise caused by the random kinetic energy of air molecules.
References:
[2] L. J. Sivian, S.D. White. On minimum audible sound field. 2015.